搜索到
4
篇与
的结果
-
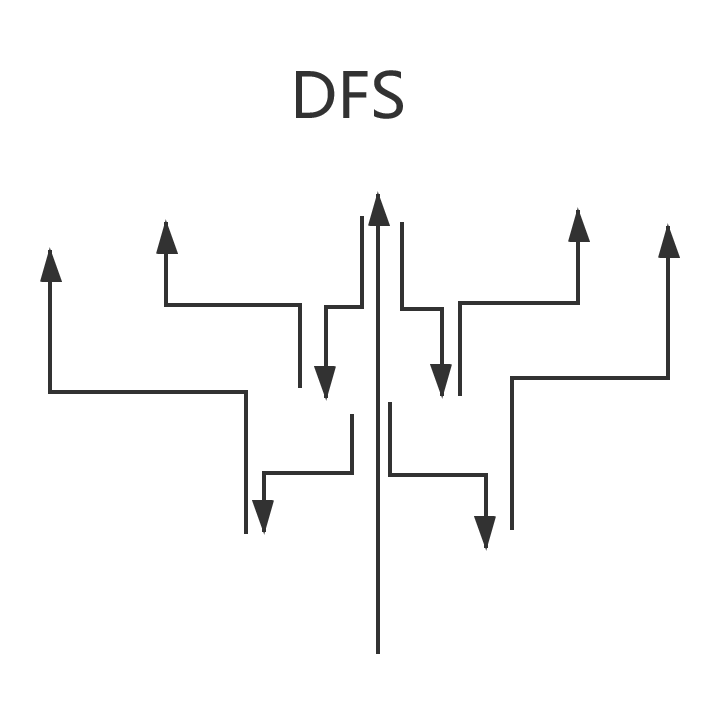
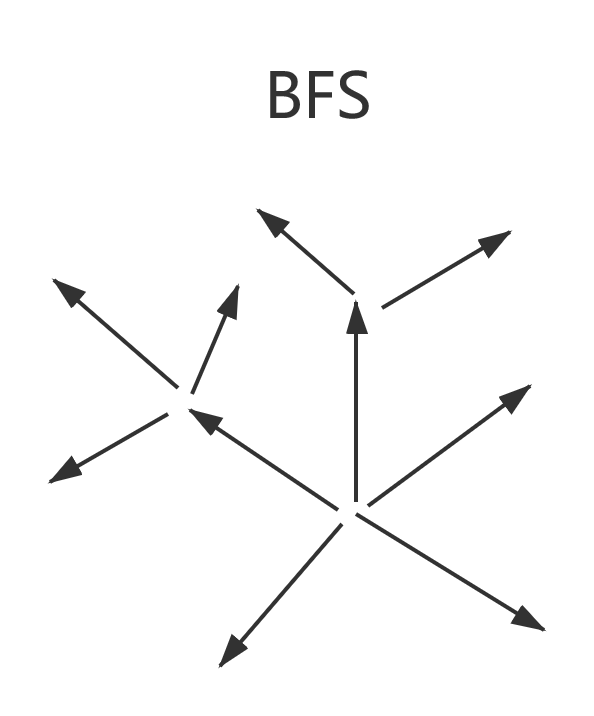
一文弄懂搜索算法中的DFS和BFS 0x01.前序有一位小伙伴问我，迷宫问题怎么解决，我说DFS或者BFS，然后，TA 说，哦哦，这我知道，就是图里面的算法嘛，但，这是个迷宫，难道我要把这个二维矩阵变成图嘛？我：当场去世。。。 于是我开启了我的长篇大论。。。希望大家有所收获。0x02.DFS和BFS简要介绍首先，回答一下那位小伙伴的问题，这个算法确实属于图里面的算法，但并不是说是专门针对图的算法，它在算法领域应用非常广泛，可以说是一种不可缺少的思想。官方说明：DFS：深度优先搜索是一种在开发爬虫早期使用较多的方法。它的目的是要达到被搜索结构的叶结点(即那些不包含任何超链的HTML文件) 。在一个HTML文件中，当一个超链被选择后，被链接的HTML文件将执行深度优先搜索，即在搜索其余的超链结果之前必须先完整地搜索单独的一条链。深度优先搜索沿着HTML文件上的超链走到不能再深入为止，然后返回到某一个HTML文件，再继续选择该HTML文件中的其他超链。当不再有其他超链可选择时，说明搜索已经结束。BFS：宽度优先搜索算法（又称广度优先搜索）是最简便的图的搜索算法之一，这一算法也是很多重要的图的算法的原型。Dijkstra单源最短路径算法和Prim最小生成树算法都采用了和宽度优先搜索类似的思想。其别名又叫BFS，属于一种盲目搜寻法，目的是系统地展开并检查图中的所有节点，以找寻结果。换句话说，它并不考虑结果的可能位置，彻底地搜索整张图，直到找到结果为止。简要理解：说实话，我第一次看没看懂，确实比较官方，我们可以用我们的思维去简单的理解一下：DFS：深度优先搜索，是一种搜索算法，讲究搜索的深度，所以叫深度优先算法。又叫回溯算法。这个算法的核心就是不断的往更深的地方搜索，如果更深的地方搜索失败了，就返回来搜，是一个回溯的过程。BFS：广度优先搜素，也是一种搜索算法，讲究搜索的广度，所以叫广度优先算法。这个算法的核心就是，先把周围的找完，再去找更深的地方。- 通俗易懂的说法：DFS就是一条路走到底，发现没路了，返回来，走另一条路。BFS就是每条路都走一点，走一点点后就走另一条路了。不如看张图，看图吧： 如果你还对这两种方式不理解，你可以看一下。0x03.DFS和BFS的实现方式这两种算法的不同主要在于优先级的不同，所以实现方式是很相似的。这两种算法都可以使用的递归的方式，其中DFS还可以用栈来实现，BFS还可以用队列实现。具体的实现，可以参考 ：DFS和BFS用递归实现的思路：根据各自传参的优先级的顺序，不断的调用自身。- 一般情况下，用递归实现BFS比较为难，所以常用队列实现。DFS用栈实现的思路：每遇到一个元素，就把这个元素的所有邻接元素入栈，当栈不为空的时候，不断的从栈顶拿出元素进行操作，直到栈为空。BFS用队列实现的思路：每遇到一个元素，就把这个元素的所有邻接元素放入队列，当队列不为空的时候，不断从队首拿出元素进行操作，直到队列为空。特别的：在非递归的实现中，你只需要把DFS的栈全部改为队列，它就变成BFS了哦~0x04.DFS和BFS的应用区别其实，大部分问题都是既可以用BFS，也可以用DFS的，但是这两种算法面对不同的问题，解决效率并不一样。BFS类似于水波纹的扩散，在求解一些最短路径，最优值问题的时候效率很高。BFS为了遍历，需要保存所有的状态，对空间来说是一个巨大的消耗。（因为通常是无法递归实现的）DFS主要应用于回溯的搜索问题中，比如迷宫问题，岛屿问题。DFS能够做到使用一个状态变量去搜索所有的状态空间，这对空间的消耗来说，是非常节约空间的（通常使用递归实现）。0x05.如何根据问题选择实现方式我的观点就是：无特殊情况，DFS就用递归实现，BFS就用队列实现。我们看一下两种实现方式对处理问题带来的不同：使用递归的方式对于恢复状态非常方便，因为大部分问题在回溯后都需要恢复相应的状态使用非递归方式对于一些求值问题来说，比较容易理解的产生原理。递归可能消耗时间会多一些。使用栈和队列可能空间消耗会非常大。非递归实现的解决问题方式，一目了然，比较容易看懂。递归解决，如果你对递归的调用过程还不是非常清晰的时候，可能就比较难理解。DFS无特殊情况就使用递归的原因是，递归更能体现这种回溯的思路。BFS无特殊情况就使用对垒实现的原因是，一般递归实现会比较难。0x06.如何使用这两种算法去解决相应的问题第一步，确定什么问题可以用这两种算法解决：（可别说只针对图了啊）凡是在一个二维矩阵中，找路径，找方法数，搜索东西，想都不要想，一般都可以用上。- 去遍历图肯定是可以的看到有关找方法的问题，可以尝试使用。- 凡是包含搜索思想的，都可以使用。第二步，确定使用的算法和实现形式，具体看上文。第三步，根据题目的需求，确定搜索失败后是否需要还原状态，求值问题是否需要更新值。第四步，设计针对性的算法。注意事项：关于求种数问题，一定要明白，每一步递归返回值的含义。- 求最短路径问题，搜索失败后，一定要还原状态，比如某些标志遍历，或者矩阵里的坐标之类的。调试小技巧：通过输出关键操作的值，来确定程序执行的顺序，确定出错原因。0x07.常用的优化算法的思路我们设计算法，不是为了单纯AC问题，而是，追求极致，比如，这个： 优化时间的思路：过滤没有必要的递归。- 合适的使用相应的数据结构。- 传参的时候传实参（指针或者引用），如果传形参会造成反复拷贝参数，如果参数过大的话，会超出时间限制。优化空间的思路：在需要恢复状态的时候，可以采用沉岛思想，不过需要题目适用。- 沉岛思想的关键是把已经访问过的值，变成一些完全不可能的值，避免重复访问，也可以根据是否需要恢复状态，考虑是否可以直接删去。0x07.谈谈它们的鼻祖这两种算法的鼻祖就是搜索算法，搜索算法的核心就是遍历到所有可能的情况，所以，常见的暴力枚举也是搜索算法的一种，所以我们在采用这两种算法的时候，思路就已经是在遍历所有可能的情况了，但是在这其中，可以借助贪心的思维去优化，做到不必要遍历每种情况。0x08.如何快速提升使用它们的能力算法，还是要使用，所有，多练习经典的题目吧！！！ 下面是一些比较经典的题目，你也可以尝试去做N皇后问题，迷宫问题。最后，多练多收获！！！
-
C++ 中的各种进制转换函数汇总 一，指定格式输出1.在C中，按指定进制格式输出如下，printf("%05o\n",35); //按八进制格式输出，保留5位高位补零 printf("%03d\n",35); //按十进制格式输出，保留3位高位补零 printf("%05x\n",35); //按十六进制格式输出，保留5位高位补零2.在C++中，按指定进制格式输出如下，#include <bitset> #include<iostream> using namespace std; int main() { cout << "35的8进制:" << std::oct << 35<< endl; cout << "35的10进制:" << std::dec << 35 << endl; cout << "35的16进制:" << std::hex << 35 << endl; cout << "35的2进制:" << bitset<8>(35) << endl; //<8>：表示保留8位输出 return 0; }二，C/C++各种进制转换库函数一）任意2-36进制数转化为10进制数。建议自己写函数，代码如下：int Atoi(string s,int radix) //s是给定的radix进制字符串 { int ans=0; for(int i=0;i<s.size();i++) { char t=s[i]; if(t>='0'&&t<='9') ans=ans*radix+t-'0'; else ans=ans*radix+t-'a'+10; } return ans; } 1.strtol()函数（） 函数原型：long int strtol(const char nptr, char *endptr, int base) base是要转化的数的进制，非法字符会赋值给endptr，nptr是要转化的字符，例如: #include<cstdio> int main() { char buffer[20]="10549stend#12"; char *stop; int ans=strtol(buffer, &stop, 8); //将八进制数1054转成十进制，后面均为非法字符 printf("%d\n",ans); printf("%s\n", stop); return 0; } 输出结果：5569stend#12 注意： ①如果base为0，且字符串不是以0x(或者0X)开头，则按十进制进行转化。 ②如果base为0或者16，并且字符串以0x（或者0X）开头，那么，x（或者X）被忽略，字符串按16进制转化。 ③如果base不等于0和16，并且字符串以0x(或者0X)开头，那么x被视为非法字符。 ④对于nptr指向的字符串，其开头和结尾处的空格被忽视，字符串中间的空格被视为非法字符。二）将10进制数转换为任意的n进制数，结果为char型。建议自己写，代码如下：string intToA(int n,int radix) //n是待转数字，radix是指定的进制 { string ans=""; do{ int t=n%radix; if(t>=0&&t<=9) ans+=t+'0'; else ans+=t-10+'a'; n/=radix; }while(n!=0); //使用do{}while（）以防止输入为0的情况 reverse(ans.begin(),ans.end()); return ans; } 1.itoa()函数（可以将一个10进制数转换为任意的2-36进制字符串） 函数原型：char*itoa(`int value,char*string,`int radix); 例如：itoa(num, str, 2); num是一个int型的，是要转化的10进制数，str是转化结果，后面的值为目标进制。#include<cstdio> #include<cstdlib> int main() { int num = 10; char str[100]; _itoa(num, str, 2); //c++中一般用_itoa，用itoa也行, printf("%s\n", str); return 0; }2.sprintf()函数（可以将一个10进制数转换为指定格式的n进制字符串）函数原型：int sprintf( char buffer, const char format, [ argument] … );#include<cstdio> int main() { char s[100]={0}; sprintf(s, "%d", 123); //十进制输出产生"123" sprintf(s, "%4d%4d", 123, 4567); //指定宽度不足的左边补空格，产生：" 1234567" sprintf(s, "%8o", 123); //八进制输出，宽度占8个位置 sprintf(s, "%8x", 4567); //小写16 进制，宽度占8 个位置，右对齐 sprintf(s, "%10.3f", 3.1415626); //产生：" 3.142" int i = 100; sprintf(s, "%.2f", i); //注意这是不对的 sprintf(s, "%.2f", (double)i); //要按照这种方式才行 return 0; }三）使用字符串流stringstream(头文件#include<sstream>) 1.将八，十六进制转十进制。#include<iostream> #include<string> #include<sstream> using namespace std; int main(void) { string s="20"; int a; stringstream ss; ss<<hex<<s; //以16进制读入流中 ss>>a; //10进制int型输出 cout<<a<<endl; return 0; } //输出：322.将十进制转八，十六进制。#include<cstdio> #include<iostream> #include<string> #include<sstream> using namespace std; int main(void) { string s1,s2; int a=30; stringstream ss; ss<<oct<<a; //10进制转成八进制读入流中，再以字符串输出 ss>>s1; cout<<s1<<endl; //输出：36 ss.clear(); //不清空可能会出错。 ss<<hex<<a; //10进制转成十六进制读入流中，，再以字符串输出 ss>>s2; cout<<s2<<endl; //输出：1e return 0; }
-
C++ 中全排列枚举的几种实现方式 1.DFS（使用递归与回溯实现）对于普通数组Array，这里给出函数模板形式：#include<bits/stdc++.h> using namespace std; template<class T> void func(T* arr, int total, int k = 0) //轮流更换第n位和n到total-1位 { for (int i = k; i < total; i++) { if (k == total - 1) //在此对排列好的数组进行下一步操作 { for (int p = 0; p < total; p++)cout << arr[p]; cout << "\n"; return; } {T t = arr[i]; arr[i] = arr[k]; arr[k] = t; }//swap(a[k],a[i]); func(arr, total, k + 1); {T t = arr[i]; arr[i] = arr[k]; arr[k] = t; } } } int main() { int arr[]{ 1,2,3,4,5 }; func(arr, 5); char crr[] = "ABCDEFG"; func(crr, 4); return 0; }对于字符串，则可跳过回溯步骤，相应地，空间复杂度将由O(1)提升至O( n! )，具体实现如下：#include<bits/stdc++.h> using namespace std; void f(string& str, int n = 0) { if (n == str.size() - 1)cout << str << endl; //在此对排列好的数组进行下一步操作 for (int i = n; i < str.size(); ++i) { string ts = str; auto t = ts[i]; ts[i] = ts[n]; ts[n] = t; f(ts, n + 1); } } int main() { return 0; string str = "1234567890"; f(str); return 0; }2.调用 algorithm.h 中的next_permutation ()函数伪代码如下：do { // todo } while (next_permutation(a, a + n));其中a为数组首地址，n为数组大小；对于string或vector，在参数中传入首末迭代器即可。
-
C++ 最大公约数函数__gcd()的用法及其朴素实现 C++的标准库中提供了一些实用的函数，比如：__gcd(x,y)函数 用于求x，y的最大公约数其中x,y不能是浮点数头文件：#include;用法：#include<iostream> #include<algorithm> using namespace std; int main() { int a,b; cin>>a>>b; cout<<__gcd(a,b)<<endl; }朴素实现方法：算法的本质是辗转相除：1.普通循环int gcd(int x,int y) { int r; while (a%b!=0) { r=a%b; a=b; b=r; } return b; }2.递归+三元运算符int gcd(int a,int b) { return b>0 ? gcd(b,a%b):a; }3.递归+ if 语句求x 和 y 的最大公约数，就是求 y 和 x % y 的最大公约数int gcd(int a,int b) { if(a%b==0) return b; else return (gcd(b,a%b)); }
